Blue Aurora didn't mention the Ellsberg Paradox specifically, but it is a major critique of subjective effective utility, and it's one that he's brought up here before.
I'm not sure, though, that it's all that much of a paradox. I'll yank the description straight from Wikipedia:
"Suppose you have an urn containing 30 red balls and 60 other balls that are either black or yellow. You don't know how many black or how many yellow balls there are, but that the total number of black balls plus the total number of yellow equals 60. The balls are well mixed so that each individual ball is as likely to be drawn as any other. You are now given a choice between two gambles:
Gamble A : You receive $100 if you draw a red ball
Gamble B: You receive $100 if you draw a black ball
Also you are given the choice between these two gambles (about a different draw from the same urn):
Gamble C: You receive $100 if you draw a red or yellow ball
Gamble D: You receive $100 if you draw a black or yellow ball
...Utility theory models the choice by assuming that in choosing between these gambles, people assume a probability that the non-red balls are yellow versus black, and then compute the expected utility of the two gambles. Since the prizes are exactly the same, it follows that you will prefer Gamble A to Gamble B if and only if you believe that drawing a red ball is more likely than drawing a black ball (according to expected utility theory). Also, there would be no clear preference between the choices if you thought that a red ball was as likely as a black ball.
Similarly it follows that you will prefer Gamble C to Gamble D if, and only if, you believe that drawing a red or yellow ball is more likely than drawing a black or yellow ball. It might seem intuitive that, if drawing a red ball is more likely than drawing a black ball, then drawing a red or yellow ball is also more likely than drawing a black or yellow ball. So, supposing you prefer Gamble A to Gamble B, it follows that you will also prefer Gamble C to Gamble D. And, supposing instead that you prefer Gamble B to Gamble A, it follows that you will also prefer Gamble D to Gamble C.
When surveyed, however, most people strictly prefer Gamble A to Gamble B and Gamble D to Gamble C. Therefore, some assumptions of the expected utility theory are violated."
The math of the paradox goes like this (also straight from Wikipedia):
So we have an apparent contradiction if you choose both A and D (I would choose both A and D, by the way).
Now, I suppose this does contradict the simple way that subjective utility is often introduced. But I don't see any way around introducing a concept in a simpler way. The ultimate point is this: we make judgements based on expected utilities associated with uncertain outcomes, not on the utility of the expectation of an outcome. In other words (as in the math above), we maximize:
P*(U(X')) + (1-P)*(U(X'')), not
U(P*X' + (1-P)*X'')
And normally that's enough to figure it out. But in this case you have to remember that the probability of a black or a yellow ball can't be treated the same as the probability of a red ball (the way the math in Wikipedia presents it). We have uncertainty about the value of B and Y, whereas we don't have uncertainty about the value of R (we only have uncertainty about whether a particular ball choice will be red, not what the probability of that event is).
Gamble D is the inverse of gamble A. We are uncertain about the value of B or Y individually, but we are positive what the value of B + Y is. It is 1-R (or 2R).
I have to confess I played with the math substituting this in and it kept coming out to the same solution. so I'm not sure that's the best way to go about it. The way to go about it, I think, is to note that R is fundamentally different from B or Y, insofar as every possible value for B and Y we could expect has probability distributions of their own. So the math on Wikipedia is actually not the right math that application of SEU would require, because we are only taking the expected value that a ball is black, and not the expected value of the probability that the ball is black (which is an additional uncertainty in this example).
Presumably you'd go about proving this more rigorously by fitting a probability distribution to B and Y, but assigning a probability of 1 to R = 1/3.


![R [U(\$100) - U(\$0)] > B [U(\$100) - U(\$0)]](http://upload.wikimedia.org/math/c/9/1/c9139b2cd4844f27f375c15ba5fc3b22.png)
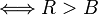

![B [U(\$100) - U(\$0)] > R [U(\$100) - U(\$0)]](http://upload.wikimedia.org/math/e/8/8/e88727eb42e2e20a1dde6ec51f02e0d0.png)





I believe that Ellsberg paradox is really a paradox. You are saying that instead of considering three states of the world, it's more correct to consider wider set of states that distinguishes between actual proportions of balls in the urn (e.g. one possible state would be: 15 black balls, 45 yellow balls and yellow ball is drawn). But this should lead to same result, since the outcome depends only on the color of drawn ball - so even if we assumed that we have subjective prior on all 183 possible states (61 distributions times 3 draws), the expected utility would collapse to the weighted sum of just three possible outcomes, with the weights given by combining subjective probabilities on black-yellow distributions and objective conditional probabilities of drawing the ball (given the distribution). This is related to (or the same as?) the reduction of compound lotteries, which is a property of expected utility.
ReplyDeleteBy the way, dealing with this is one of active research areas these days, with applications in macroeconomics and finance, just search for "robustness" or "ambiguity aversion". One possible approach to rationalizing Ellsberg paradox (proposed by Gilboa & Schmeidler)is to assume that people have set of priors, and make their choices to maximize the worst possible outcome (across priors) - so bet B could be evaluated with prior that there are zero black balls, and bet C with prior that there are zero yellow balls, and thus bets A, D would be preferred.
Hmm, Krugman properly referred to the "subjunctive" (mood). Maybe I have misjudged him.
ReplyDeleteMaybe this is a naive question (there's your opening Bob!) but aren't both preferences, A>B, D>C what we would see from someone who feared the experimenter was going to diddle him? In A I have a guaranteed 1/3 chance with A, but if there's a trick here and I'm being diddled, option B might correspond to a 0% chance. I'm vulnerable to a fraud.
ReplyDeleteI get the point about equal values etc. I am suggesting there might be a psychological effect at work here: avoid the choice that could be rigged against me.
Important point. Human intelligence evolved in a social environment, in which you cannot trust the person who gives you the choice. Maybe you can trust him about the number of balls and the colors, since they are verifiable. But you can't trust him not to try to take advantage of your guess about the unspecified numbers.
DeleteDuring an interview after he had retired, Monty Hall was asked about the Monty Hall Problem. He had never heard of it, he said, but he could always manipulate people to make the choice he wanted them to.
Part of the point of the Ellsberg paradox, if I have this down right, is that people are in theory supposed to favour both options equally 50-50. Instead, there is ambiguity aversion, Daniel. Not risk aversion. There's an important difference.
ReplyDeleteThe usual assumption would be that one should be indifferent between the two, as you say, but Ellsberg also rules out a range of other theories, thus demonstrating that there is not just risk aversion here.
DeleteP.S. Do you think they understood your question? Or answered it? Both seemed to think that SEU was somehow sensible, it was just that people didn't abide by it. Ellsberg seems to show that the narrow notion of probability in SEU is too limited, and needs extending in something like the way that Daniel K suggests.
I say more below.
There is an extra dimension of risk in both B and C. In A, there are exactly 30 balls; in D, there are exactly 60 balls. B contains risk (avg 30, positive variance), as does C (avg 60, positive variance). If people are averse to the variance of outcomes, they would prefer A and D; if they are risk loving they would prefer B and C. If you make utility decreasing with variance of outcomes, this result pops out. The flaw is assuming that people have preferences over the color of balls, rather than a preference over the certainty of the outcome.
ReplyDeleteI agree with all this except the last sentence.
DeleteThe thing is, SEU incorporates utility that declines with variance. That's why we maximize the expected utility and not the utility of the expected outcome.
What I think this "paradox" misses is what you point out - that there is variability (that people presumably care about) in the probabilities themselves rather than just in the outcomes.
Ellsberg types say "you should worry about this concern over variability". Me and other SEU types say "ummm... we do".
This is an important issue. Could you be more explicit about you model of utility? What Ellsberg is criticising is the usual definition under which the alternatives you cite are assumed to be the same.
ReplyDeleteAt http://djmarsay.wordpress.com/bibliography/rationality-and-uncertainty/broader-uncertainty/ellsbergs-risk/ I note that Ellsberg's paradox can be resolved by replacing conventional probability by a Boolean probability. I wonder if your notion is equivalent, or new.